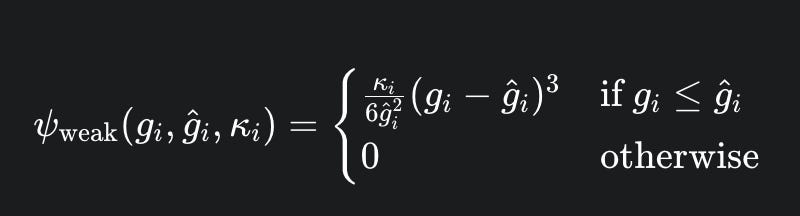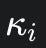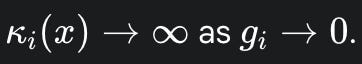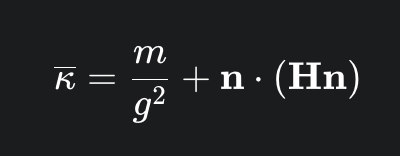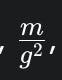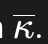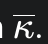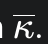Paradigms of Motion: A Comparative Analysis of Physics-Based Simulation and Generative AI at the Cutting Edge of Video Modeling

A quick revisit to technical analysis and deep research

Good ole phsyics modeling or gen AI? Find out today in the analysis of the latest cutting edge papers on generative video.

See: A Cubic Barrier with Elasticity-Inclusive Dynamic Stiffness

Also see: Tiktok technical analysis

Executive Summary

The field of digital video modeling is currently defined by two powerful, yet fundamentally distinct, paradigms. The first, rooted in the principles of computational physics, seeks to generate motion by explicitly simulating the underlying physical laws that govern the world. This approach prioritizes accuracy, determinism, and fine-grained control, with the state of the art focused on solving long-standing challenges in contact resolution and numerical stability for increasingly complex scenarios. A recent breakthrough in this domain, a novel cubic barrier function combined with an elasticity-inclusive dynamic stiffness, demonstrates unprecedented scalability in handling massive, contact-rich simulations, pushing the boundaries of what is computationally feasible while making a pragmatic trade-off between absolute mathematical convergence and robust visual performance.

The second paradigm is that of generative artificial intelligence, which learns to synthesize video by identifying and replicating patterns within vast datasets of visual information. This data-driven approach, spearheaded by architectures like the Diffusion Transformer, has achieved remarkable success in generating visually plausible and creatively flexible video content from simple text or image prompts. Leading models such as OpenAI’s Sora and Google’s Lumiere showcase emergent capabilities, including an implicit understanding of 3D space, object permanence, and basic physical interactions. The primary innovation in this space revolves around novel methods for representing and maintaining temporal coherence, with a strategic shift in ambition from mere content creation to the development of “world simulators” capable of predictive reasoning.

This report provides an exhaustive comparative analysis of these two paradigms. It deconstructs the mathematical and algorithmic underpinnings of the physics-based approach, highlighting its strengths in predictability and control, as well as its limitations in authoring complexity and handling extreme physical parameters. It then dissects the architectural foundations of leading generative models, examining their capabilities for emergent realism and creative expression, while also critically assessing their persistent failures in causality and physical consistency. The synthesis of these analyses reveals a core dichotomy between explicit accuracy and emergent plausibility. The future of video modeling lies not in the dominance of one paradigm over the other, but in their inevitable convergence. The emergence of hybrid, physics-informed generative models and the development of rigorous benchmarks for physical intelligence signal a new frontier where the deterministic control of simulation will be combined with the creative power of generation, paving the way for a new class of reality engines with profound implications for science, entertainment, and artificial intelligence.

---

Part I: The Paradigm of Physical Simulation - Deterministic Dynamics and Contact Resolution

The pursuit of realistic digital motion has long been anchored in the field of computational physics. This paradigm operates on the first principle that to create a believable video of a physical event, one must simulate the event itself by solving the governing equations of motion. This section provides a deep analysis of the state-of-the-art in this domain, using the recent work “A Cubic Barrier with Elasticity-Inclusive Dynamic Stiffness” by Ryoichi Ando as a primary case study.¹ This research exemplifies the modern approach to physical simulation, which is characterized by a relentless focus on overcoming the intricate challenges of contact, deformation, and numerical stability in scenarios of extreme complexity.

1.1. Foundational Challenges in Computational Physics

The simulation of deformable objects, such as cloth, shells, and soft bodies, presents a set of profound computational challenges that have occupied researchers for decades. While the fundamental laws of motion are well-understood, their application in a discrete, digital environment gives rise to significant difficulties, particularly when objects come into contact.

The Problem of Contact

At the heart of physical simulation lies the problem of contact resolution. It is a non-negotiable constraint: objects in the real world do not pass through one another. Enforcing this simple rule in a simulation is extraordinarily difficult, especially for so-called “codimensional colliders” like thin shells or strands of hair.¹ Unlike volumetric objects, these have no meaningful interior volume. Even a minuscule amount of interpenetration between two shells can create a topologically invalid state from which a solver cannot recover, causing the entire simulation to halt, trapped in a state of self-intersection.¹

To combat this, the computer graphics community developed a class of methods known as Incremental Potential Contact (IPC).¹ The core idea of IPC is to prevent penetration from ever occurring by erecting a repulsive energy barrier between objects that are in close proximity. Historically, these barriers have been logarithmic functions of the distance, or “gap,” between two objects. As the gap approaches zero, the logarithmic barrier’s energy potential approaches infinity, theoretically making it impossible for a solver to choose a state that involves penetration.¹

The Limitation of Logarithmic Barriers

While theoretically sound, the logarithmic barrier introduces a pernicious numerical artifact. The dynamics of the simulation are typically solved using an optimization method like Newton’s method, which iteratively takes steps to minimize a total energy function (comprising inertia, elasticity, and contact barrier energies). The direction of each step is determined by the system’s forces (the negative gradient of the energy) and its stiffness (the Hessian, or second derivative, of the energy).

The critical issue, first formally identified by Huang et al., arises from the mathematical nature of the logarithmic function.¹ As the gap between two objects approaches zero, the curvature (the second derivative) of the logarithmic barrier energy grows hyperbolically toward infinity. When the solver calculates the next step, it effectively divides the contact force by this immense curvature. The result is a search direction of extremely small, often sub-floating-point-precision, magnitude.¹ This phenomenon, termed “search direction locking,” causes the solver to become stuck, unable to make meaningful progress to separate the nearly-touching objects, even though a strong repulsive force is present. The simulation effectively freezes, not because of a topological error, but because of a numerical one. Proposed solutions, such as clamping the curvature, avoid the locking but can produce excessively large and unstable search directions.¹

Strain Limiting and Numerical Instability

A related challenge is strain limiting, a technique essential for simulating materials like cloth or paper that resist stretching.¹ Strain limiting is also implemented as a constraint, often using the same barrier-based methods as contact handling. A constraint might specify that the deformation of a triangular mesh element cannot exceed, for example, 5% of its resting state. When a simulation involves both tight strain limiting and numerous contacts—such as a sheet of paper crumpling—the system becomes extraordinarily “stiff.” Small changes in vertex positions can lead to enormous changes in the total energy. This extreme stiffness further pollutes the conditioning of the system’s Hessian matrix, making it exceptionally difficult for iterative solvers like the Preconditioned Conjugate Gradient (PCG) method to converge to a solution, thereby compounding the instability introduced by contact barriers.¹

1.2. A Novel Approach: The Cubic Barrier Function

In response to the fundamental limitations of logarithmic barriers, Ando’s work introduces a new type of barrier function with a carefully chosen mathematical form designed to circumvent the problem of search direction locking.¹

Mathematical Formulation

The proposed barrier begins as a “weak” cubic energy potential,

defined by the following equation ¹:

Here, $g_i$ represents the gap distance for a given constraint is the activation distance at which the barrier becomes active, and is a stiffness coefficient. The key mathematical property of this function is that it is C^2 continuous. This means that not only the energy and its first derivative (force) are continuous at the activation gap, but its second derivative (curvature or stiffness) is also continuous, smoothly transitioning to zero.¹

Solving Search Direction Locking

The choice of a cubic function is deliberate and elegant. Unlike a logarithmic barrier, whose curvature explodes as the gap approaches zero, the curvature of this cubic barrier is a simple linear function of the gap. As $g_i$ approaches zero, the curvature approaches a finite, non-zero value. This property is the central mechanism for defeating search direction locking. Because the curvature remains well-behaved and moderate near the critical point of contact, the resulting search directions computed by the Newton solver are neither vanishingly small nor excessively large.¹ This allows the solver to continue making meaningful, stable progress in resolving near-contact states where logarithmic barriers would have stalled. The paper demonstrates that this property is particularly effective for the extremely small gaps encountered in tight strain limiting scenarios.¹

The Inherent Trade-Off

The adoption of this cubic function, however, comes at a significant cost. It is termed a “weak” barrier because it fundamentally abandons the most desirable theoretical property of traditional IPC: the guarantee of an infinite energy potential at zero gap.¹ A finite barrier energy means that, in principle, a solver could find it energetically favorable to allow penetration if other forces in the system (like inertia) are sufficiently large. This trade-off is a critical one: the method gains numerical stability and avoids locking, but it loses the hard, built-in guarantee against intersection that defined the previous generation of robust simulators. This decision introduces a new challenge that the remainder of the methodology must address: if the barrier itself is not infinitely strong, how can penetration be reliably prevented?

1.3. Dynamic Stiffness and Semi-Implicit Evaluation

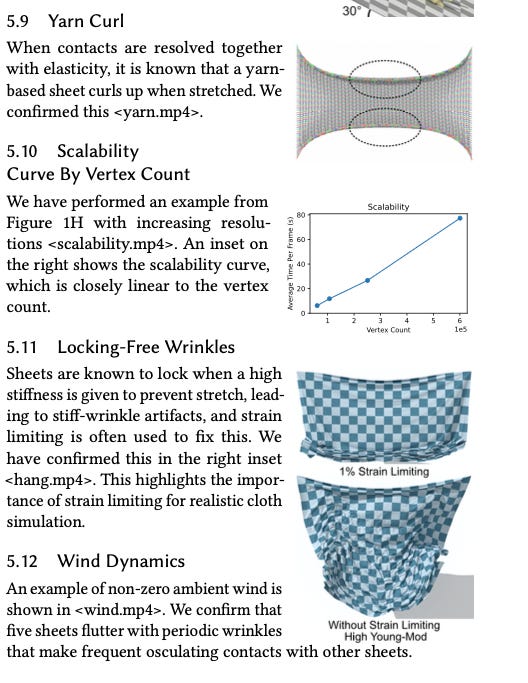
Having replaced the infinitely stiff logarithmic barrier with a numerically stable but finite cubic one, the research then introduces its second major innovation: a new method for calculating the stiffness coefficient, $kappa_i$ (), that is both physically informed and computationally robust.¹

The Concept of Elasticity-Inclusive Stiffness

The naive attempt to restore the “infinite barrier” property would be to make the stiffness

itself a function of the gap, such that

However, as the paper notes, this reintroduces the very search direction locking problem the cubic barrier was designed to solve.¹

The proposed solution is far more sophisticated. It redefines stiffness not just as a function of distance, but as a combination of a distance-based term and a material-property-based term. This “elasticity-inclusive” stiffness is governed by the principle that the contact barrier should be at least as stiff as the objects it is trying to keep apart. The governing equation for the stiffness of a given constraint is ¹:

This equation has two components. The first term,

is a reactive, distance-based stiffness. As the gap $g$ shrinks, this term ensures the barrier’s strength increases quadratically, eventually becoming strong enough to counteract any opposing forces.

The second term,

is the novel, proactive component. Here, H is the Hessian matrix of the object’s internal elastic energy (e.g., hyper-elasticity and bending), and n is the direction of interest, such as the contact normal. This term calculates the effective stiffness of the deformable body itself in the specific direction of the contact. By incorporating the material’s own elasticity Hessian into the contact stiffness, the barrier can “feel” how stiff the colliding objects are. A collision with a stiff material will generate a correspondingly stiffer barrier, proactively resisting deformation and penetration well before the gap becomes critically small. This is a more physically-informed approach than one based solely on geometric proximity.

The Semi-Implicit Breakthrough

The crucial element that makes this dynamic stiffness viable is the use of a semi-implicit evaluation, denoted by the bar notation

The term “semi-implicit” here means that when the solver computes the derivatives (force and Hessian) of the total energy potential within a single Newton step, the value of

is treated as a pre-computed constant. It is only updated between Newton steps.¹

This decoupling is the central algorithmic innovation that resolves the conflict between a dynamic stiffness and a stable solver.

Although

depends on the current state (gap distance $g$ and the elasticity Hessian H), by freezing its value during the differentiation process, the method avoids introducing the complex higher-order derivatives and dependencies that would lead to search direction locking.¹ This two-part solution is highly effective: the cubic function provides a mathematically stable shape for the local energy landscape that the solver must navigate, while the semi-implicitly updated dynamic stiffness provides the necessary repulsive force to ensure physical correctness, without corrupting the solver’s search direction.

Simulation Step Algorithm

Advantages over IPC

This novel stiffness selection mechanism confers several distinct advantages over the methods used in traditional IPC.¹ First, it is entirely parameter-free. It does not rely on heuristically chosen “magic numbers” (such as 10^{11} or 100) to define stiffness, instead deriving it from the physical properties of the system (mass, gap, elasticity). Second, it requires no manually set lower or upper bounds for stiffness, nor does it need fail-safe mechanisms like doubling the stiffness when a simulation is struggling. The stiffness adapts automatically and robustly, enlarging the contact gap by providing just enough resistance to prevent penetration without becoming unnecessarily stiff and destabilizing the system.¹

1.4. Performance Under Extreme Conditions

The value of a simulation method is ultimately measured by its performance on challenging, large-scale problems. The presented research validates its approach through a series of demanding benchmarks designed to push the limits of contact-rich simulation. This represents a philosophical shift in high-end simulation, moving from a focus on “guaranteed correctness” in simpler scenarios to “robust performance” at massive scale. While traditional IPC offers a hard mathematical guarantee of intersection-free results, this new method opts for an inexact, projective approach that is demonstrably more scalable and stable for the kind of chaotic, complex scenes often required in high-end visual effects, prioritizing visual plausibility and performance over strict, gradient-vanishing convergence.

Scalability to Massive Contact Scenarios

The results demonstrate remarkable scalability. The “Five Cylinders Twisted” example, which involves five cylindrical shells being twisted and bundled together, peaks at an astonishing 168.35 million simultaneous contacts.¹ Even under this extreme load, the average time to compute a single video frame is 194 seconds. Another example, “Squishy Balls,” features eight soft bodies with 6.40 million vertices being compressed in a container, a scenario involving both massive deformation and widespread contact, which is handled stably.¹ These figures show that the method can handle contact densities and geometric complexity far beyond what was previously considered tractable for implicit solvers.